Experiments with psychedelic, colour-changing fibres and spaghetti might sound more akin to child's play than to serious scientific research, but a team of mathematicians and engineers at Massachusetts Institute of Technology in Boston have slowly disentangled the Gordian knot of understanding the factors which determine knot strength, using pressure-sensing fibres to develop a new mathematical model - with some help from everyone's favourite stringy carbohydrate. The team hope that their findings outlined in the paper 'Topological mechanics of knots and tangles' could help match particular knots to specific safety purposes in climbing, sailing and rope access work.

Although mathematicians have long studied the theory of knots, or knot theory, the mechanics of what makes certain knots stronger or better-suited to different applications over others remained unknown. 'Knot theory in mathematics is the study of knotted closed curves in space, and is interested in questions such as when two curves represent the same knot,' MIT PhD student and first author of the study, Vishal Patil, explains. 'For example, one central problem in knot theory is how to tell whether a given curve is knotted or not in the first place. It turns out that this problem is quite tricky - if I give you a complicated, tangled-up curve, there's no easy way to tell if it's knotted.' Knot theory uses diagrams and equations involving quantities of link and writhe to 'describe' a knot. While this theory focuses on classifying entanglements, only a few studies had considered the physics of stress, strain and friction within knots.

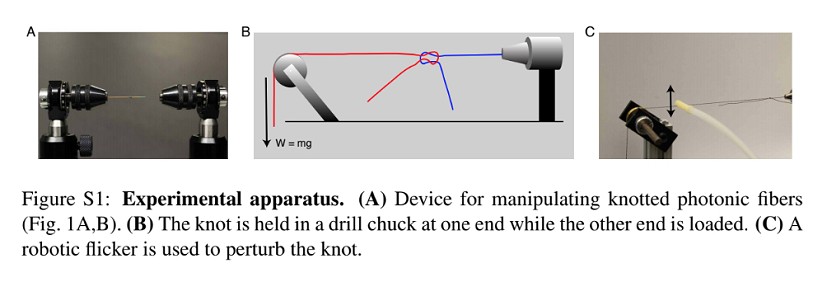
How could this mathematical theory be further experimented with and tested in practice? In 2013, Mathias Kolle, Associate Professor at MIT, and PhD student Joseph Sandt developed pressure-sensing photonic fibres which change colour when stretched. The fibres consist of layers of elastic rubber, each with different material properties which affect their refractive indices, or how they interact with light. Under varying degrees of pressure, new layers with different refractive properties and therefore colour indications are unveiled. In their chosen colourmap, areas of green and yellow indicated high strain, while red and orange zones were under low stretch. The practical applications of these fibres attracted the attention of the mathematicians tying themselves in knots over the theory, and an obvious opportunity to pull together - so to speak - and join forces in collaboration arose.

Using this visual indicator, the team built a virtual model and calibrated it according to the colour spectrum of the physical fibres, inspired by a model devised for an earlier paper researching the fracture dynamics of dried spaghetti. Alongside Jörn Dunkel, associate professor of physical applied mathematics at MIT, Vishal put a very literal twist on earlier research, which found that when bent evenly from both ends, spaghetti will refuse to split in two and instead shatter into three or more fragments due to a "snap-back" effect of further vibrations. Vishal and Jörn answered a nagging question: could spaghetti be forced to break in two? Their team discovered that by twisting the dried rod past a critical degree before bending it, the spaghetti would split into two pieces. Aside from the model's relevance to their recent studies into knot strength, twisting would play an important role once again when it came to studying knot strength.

With the virtual model in place, the team used it to outline the key properties that determine a knot's stability, with a focus on bend knots. 'It's essentially a combination of three things,' Vishal says. A knot's strength hinges on:

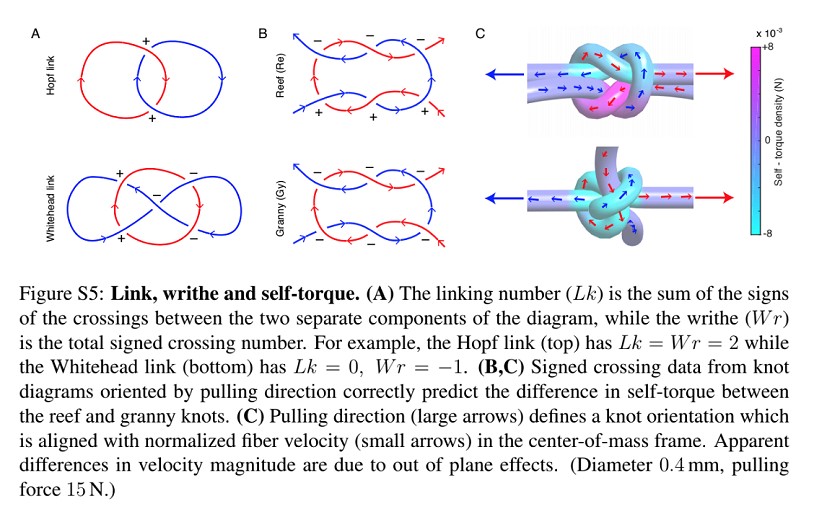
'As an example, the paper describes the difference between a granny and a reef knot, with a pictorial description of how this twist energy works to differentiate between knots,' Vishal explains. The reef knot, boasting two more twist fluctuations, is stronger than the granny - as many will have learned the hard way when learning to tie shoelaces.

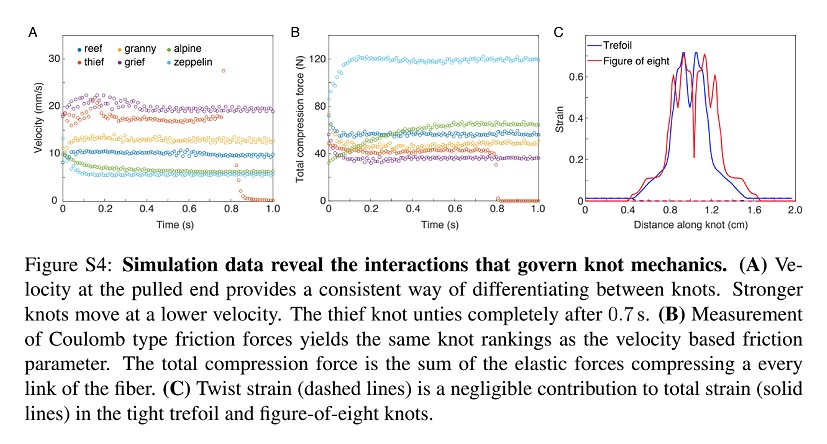
The team studied knots used to tie two pieces of rope together, or bend knots, commonly used in sailing and climbing. The following knots were tested: the reef, granny, bowline, carrick, hunter, zeppelin, ashley and butterfly.

A figure of eight is one of the most common knots in climbing and is often contested by the bowline as a tie-in knot of choice. Although the team didn't analyse the figure of eight in detail, they tied it with a colour-changing fibre and used the data to validate their simulations. Some climbers prefer to tie-in with a bowline as it's easier to untie after loading, but it's also easier to tie incorrectly without noticing. 'We looked at the bowline, which can be used as a bend (a sheet bend) and at slight variants of it. The three properties we came up with predict that some of these bowline variants will be much weaker than others when used as a bend, which backs up this idea that it's easy to tie incorrectly,' Vishal comments. 'These properties could also be used to tell whether or not you've tied the knot incorrectly.'

While the planar diagrams created by the team appear to correspond to the way the knots studied behave in reality so far, more complex knots may require 3D modelling to accurately understand the interactions between crossings and the forces involved.

Another limitation of the study is that the mathematical models don't currently take the varying friction properties of rope or other materials into account. This is an area of ongoing research, which Vishal hopes will receive more attention in future studies. 'We wanted to find high level properties of knots, which could be applied to lots of knots in different ropes. The consequence of aiming for generality is that we miss out details like rope structure,' he explains. 'It's certainly true that this needs to be taken into account to properly understand knots, and Pedro Reis is doing some interesting work in this direction.' In his lab in Lausanne, Switzerland, Pedro is currently performing sophisticated experiments using x-ray tomography to study, amongst other things, the failure of knots.

Mathias is a keen sailor and although there were no climbers on the team, they used some set-ups from these activities and applied them to tests in the lab. 'The experiment we did to test the strength of various knots was meant to mimic a real-life climbing scenario on a smaller scale,' Vishal explains. 'We tied various knots in dyneema cord, clamped one end and attached masses to the other end until the knot slipped.' These experiments confirmed the ranking of knot stability predicted by simulations, with the zeppelin knot proving to be more secure against untying than the alpine butterfly.

Some might perceive a large, complex knot as being stronger than a simpler one. However, the MIT study showed that the interplay of the three key properties combined is a better indicator of strength than having a high level of complexity, such as multiple complicated crossings, for example. 'Interestingly, it's not always true that a knot with more crossings is better than a knot with fewer crossings. Although property 1 is important, the other 2 properties matter,' Vishal says. 'One interesting thing we found is the zeppelin bend appears to be better than the alpine butterfly knot for tying two ropes together. However, given that these might be used in life or death situations in climbing, I would advocate further testing before switching the knots you're used to!'

It is hoped that as research continues, these studies could provide solid data to unravel the mysteries of more complex knots through 3D modelling, with practical safety implications for activities that rely on sturdy knots.